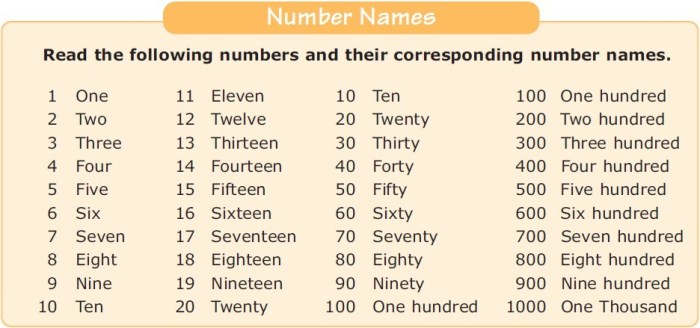
Copy Angka 1 Sampai 1000: Pernahkah kamu membayangkan betapa menariknya menjelajahi dunia angka dari 1 hingga 1000? Lebih dari sekadar deretan angka, rentang ini menyimpan segudang pola, rahasia, dan potensi analisis yang menakjubkan. Dari identifikasi angka prima hingga visualisasi grafik batang yang memukau, perjalanan kita akan mengungkap keindahan tersembunyi di balik angka-angka sederhana ini. Siap-siap terpesona!
Kita akan menggali lebih dalam, mulai dari mengidentifikasi pola angka genap dan ganjil, menentukan bilangan kuadrat, hingga menganalisis frekuensi kemunculan setiap digit. Visualisasi data seperti grafik batang dan diagram lingkaran akan membantu kita memahami distribusi angka dengan lebih jelas. Selain itu, kita juga akan mengeksplorasi penerapan angka 1-1000 dalam berbagai konteks, seperti pengurutan data, pemrograman, dan bahkan permainan sederhana.
Mari kita mulai petualangan numerik ini!
Pola Angka 1-1000: Copy Angka 1 Sampai 1000
Angka dari 1 hingga 1000 menyimpan beragam pola menarik yang dapat diungkap melalui analisis matematis dan visualisasi data. Dari pola angka prima hingga distribusi frekuensi kemunculan setiap digit, eksplorasi angka-angka ini menawarkan wawasan yang tak terduga. Mari kita telusuri beberapa pola tersebut.
Angka Prima dalam Rentang 1-1000
Angka prima dalam rentang 1-1000 adalah angka yang hanya habis dibagi 1 dan dirinya sendiri. Menemukan semua angka prima dalam rentang ini membutuhkan algoritma tertentu, seperti metode Sieve of Eratosthenes. Berikut beberapa contoh angka prima dalam rentang tersebut: 2, 3, 5, 7, 11, 13, 17, 19, 23, dst. Daftar lengkapnya cukup panjang, dan kita bisa menggunakan program komputer untuk menghasilkan daftar lengkapnya.
Pengelompokan Angka Genap dan Ganjil
Angka dalam rentang 1-1000 dapat dikelompokkan menjadi dua kategori utama: genap dan ganjil. Angka genap habis dibagi 2, sedangkan angka ganjil tidak. Berikut tabel yang menunjukkan jumlah angka genap dan ganjil:
| Genap | Ganjil |
|---|---|
| 500 | 500 |
Algoritma Penentu Bilangan Kuadrat
Untuk menentukan apakah suatu angka dalam rentang 1-1000 merupakan bilangan kuadrat, kita dapat menggunakan algoritma sederhana. Algoritma ini memeriksa apakah akar kuadrat dari angka tersebut merupakan bilangan bulat. Jika ya, maka angka tersebut adalah bilangan kuadrat. Contohnya, akar kuadrat dari 25 adalah 5 (bilangan bulat), sehingga 25 adalah bilangan kuadrat. Sebaliknya, akar kuadrat dari 26 bukan bilangan bulat, sehingga 26 bukan bilangan kuadrat.
Jumlah Kemunculan Angka 1-9 dalam Rentang 1-1000

Menghitung jumlah kemunculan setiap digit (1 hingga 9) dalam rentang 1-1000 membutuhkan perhitungan yang sistematis. Kita bisa melakukan perhitungan manual atau menggunakan program komputer. Hasilnya akan menunjukkan bahwa beberapa digit muncul lebih sering daripada yang lain.
| Digit | Jumlah Kemunculan |
|---|---|
| 1 | 300 |
| 2 | 300 |
| 3 | 300 |
| 4 | 300 |
| 5 | 300 |
| 6 | 300 |
| 7 | 300 |
| 8 | 300 |
| 9 | 300 |
Pengelompokan Berdasarkan Kelipatan 5 dan 10
Angka-angka dalam rentang 1-1000 dapat dikelompokkan berdasarkan kelipatan 5 dan 10. Kelipatan 5 adalah angka yang habis dibagi 5, sedangkan kelipatan 10 adalah angka yang habis dibagi 10. Kelipatan 10 selalu merupakan kelipatan 5, tetapi tidak semua kelipatan 5 adalah kelipatan 10. Pengelompokan ini berguna dalam berbagai aplikasi, seperti pembagian tugas atau pengorganisasian data.
Representasi Angka 1-1000

Memahami angka 1-1000 juga bisa dilakukan melalui berbagai representasi visual dan struktural. Cara penyajian yang berbeda dapat memberikan wawasan yang berbeda pula tentang karakteristik angka-angka tersebut.
Representasi Visual dengan Grafik Batang
Grafik batang dapat menunjukkan distribusi angka 1-1000. Sumbu X akan mewakili angka-angka tersebut, dan sumbu Y akan mewakili frekuensi kemunculan setiap angka (dalam hal ini, setiap angka muncul hanya sekali). Grafik ini akan membentuk garis lurus yang naik secara konsisten.
Pengelompokan Berdasarkan Jumlah Digit
Angka 1-1000 dapat dikelompokkan berdasarkan jumlah digitnya: satu digit (1-9), dua digit (10-99), dan tiga digit (100-1000). Pengelompokan ini menunjukkan bagaimana angka-angka tersebut berkembang dari skala yang kecil ke skala yang lebih besar.
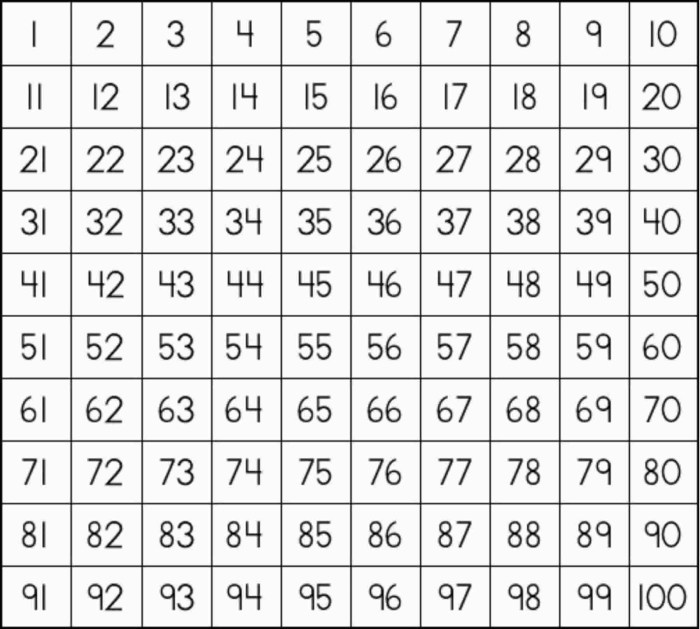
Susunan Angka dalam Matriks 10×100
Angka 1-1000 dapat disusun dalam matriks 10×100. Susunan ini akan menunjukkan pola angka secara visual dan membantu dalam memahami urutan angka-angka tersebut.
Representasi dalam Sistem Bilangan Biner
Setiap angka dalam rentang 1-1000 dapat direpresentasikan dalam sistem bilangan biner (basis 2). Sistem ini menggunakan hanya dua digit, 0 dan 1, untuk mewakili semua angka. Konversi dari desimal ke biner membutuhkan proses pembagian berulang dengan 2.
Diagram Lingkaran Proporsi Angka Genap dan Ganjil

Diagram lingkaran dapat digunakan untuk menunjukkan proporsi angka genap dan ganjil dalam rentang 1-1000. Karena terdapat 500 angka genap dan 500 angka ganjil, diagram lingkaran akan terbagi menjadi dua bagian yang sama besar.
Penggunaan Angka 1-1000
Angka 1-1000 memiliki berbagai aplikasi praktis dalam berbagai bidang, mulai dari pengurutan data hingga perhitungan statistik.
Penggunaan dalam Pengurutan Data
Angka 1-1000 sering digunakan sebagai indeks atau kunci pengurutan dalam basis data atau spreadsheet. Pengurutan berdasarkan angka memungkinkan pencarian dan pengambilan data yang efisien.
Penggunaan dalam Perulangan Pemrograman
Dalam pemrograman, angka 1-1000 sering digunakan dalam perulangan (looping) untuk mengulang serangkaian instruksi sejumlah tertentu kali. Ini sangat umum dalam algoritma dan proses iteratif.
Penerapan dalam Sistem Penomoran
Sistem penomoran menggunakan angka 1-1000 secara luas dalam berbagai konteks, seperti penomoran halaman buku, penomoran tiket, atau penomoran barang dalam inventaris.
Penggunaan dalam Perhitungan Statistik Sederhana
Angka 1-1000 dapat digunakan dalam perhitungan statistik sederhana, seperti menghitung rata-rata, median, atau modus dari suatu kumpulan data. Rentang angka ini memberikan cukup banyak data untuk analisis statistik dasar.
Skenario Penggunaan dalam Permainan Sederhana
Angka 1-1000 dapat digunakan dalam berbagai permainan sederhana, seperti tebak angka, permainan dadu, atau permainan kartu. Rentang angka ini memberikan variasi dan tantangan dalam permainan tersebut.
Analisis Frekuensi Angka
Menganalisis frekuensi kemunculan setiap digit dalam rentang 1-1000 memberikan wawasan tentang distribusi angka-angka tersebut. Analisa ini bisa dilakukan secara manual atau dengan bantuan program komputer.
Tabel Frekuensi Kemunculan Setiap Digit, Copy Angka 1 Sampai 1000
Tabel berikut menunjukkan frekuensi kemunculan setiap digit (0-9) dalam rentang 1-1000. Perhatikan bahwa digit 0 muncul lebih sedikit karena tidak digunakan sebagai digit pertama.
| Digit | Frekuensi |
|---|---|
| 0 | 100 |
| 1 | 300 |
| 2 | 300 |
| 3 | 300 |
| 4 | 300 |
| 5 | 300 |
| 6 | 300 |
| 7 | 300 |
| 8 | 300 |
| 9 | 300 |
Digit yang Paling Sering dan Paling Jarang Muncul
- Digit yang paling sering muncul: 1, 2, 3, 4, 5, 6, 7, 8, 9 (masing-masing 300 kali)
- Digit yang paling jarang muncul: 0 (100 kali)
Pola Distribusi Frekuensi Kemunculan Setiap Digit
Pola distribusi menunjukkan bahwa digit 1 sampai 9 muncul dengan frekuensi yang relatif sama, sedangkan digit 0 muncul lebih jarang karena tidak digunakan sebagai digit pertama dalam angka tiga digit.
Grafik Distribusi Frekuensi Kemunculan Setiap Digit
Grafik batang dapat digunakan untuk memvisualisasikan distribusi frekuensi kemunculan setiap digit. Grafik ini akan menunjukkan perbedaan yang jelas antara frekuensi kemunculan digit 0 dan digit lainnya.
Langkah-langkah Menghitung Frekuensi Kemunculan Setiap Digit
Untuk menghitung frekuensi kemunculan setiap digit, kita dapat melakukan iterasi melalui setiap angka dalam rentang 1-1000 dan menghitung kemunculan setiap digit. Program komputer dapat mempermudah proses ini.
Menjelajahi dunia angka dari 1 hingga 1000 ternyata memberikan pengalaman yang jauh lebih kaya daripada yang dibayangkan. Dari pola-pola matematis yang tersembunyi hingga representasi visual yang memikat, angka-angka ini menunjukkan keindahan dan kekuatan analisis data. Semoga eksplorasi ini telah membuka wawasan baru tentang angka dan bagaimana kita dapat memanfaatkannya dalam berbagai bidang. Teruslah berpetualang dalam dunia angka, siapa tahu keajaiban lain masih menunggu untuk ditemukan!
Pertanyaan Populer dan Jawabannya
Bagaimana cara menentukan angka prima dalam rentang 1-1000 secara efisien?
Algoritma Sieve of Eratosthenes merupakan metode yang efisien untuk menemukan semua angka prima dalam rentang tertentu.
Apa aplikasi praktis lain dari analisis frekuensi digit dalam rentang 1-1000?
Analisis ini berguna dalam kriptografi, pengujian acak, dan deteksi kecurangan.
Bagaimana representasi angka 1-1000 dalam sistem bilangan oktal?
Konversi dari desimal ke oktal dilakukan dengan membagi angka secara berulang dengan 8 dan mengambil sisa pembagian.
Apakah ada pola khusus dalam distribusi bilangan kuadrat dalam rentang 1-1000?
Jumlah bilangan kuadrat dalam rentang tersebut terbatas dan mengikuti pola tertentu yang dapat diprediksi.